This Benford’s Law Calculator is designed to calculate the first digit frequencies in numbers comprising a given data set and test the hypothesis for their compliance with Benford’s law. Enter the data set values in the appropriate field of this calculator and get the first digit frequency distribution. You will get also the number of input elements (dataset size), maximal and minimal values of the data set, χ²-value and P-value which are the parameters characterizing the deviation of the found frequencies from the Benford’s Law. The found frequencies are presented in graphical form along with Benford’s Law curve. You can paste the input data copied from a spreadsheet or csv-file or enter manually using comma, space or enter as separators.
Benford’s Law
Established empirically, the Benford’s law, also called the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, claims that many, but not all, data sets with a natural origin, including the results from mathematical operations, might produce relative frequencies for the first digit where the occurrence of the smaller numbers is higher than that of the larger numbers.
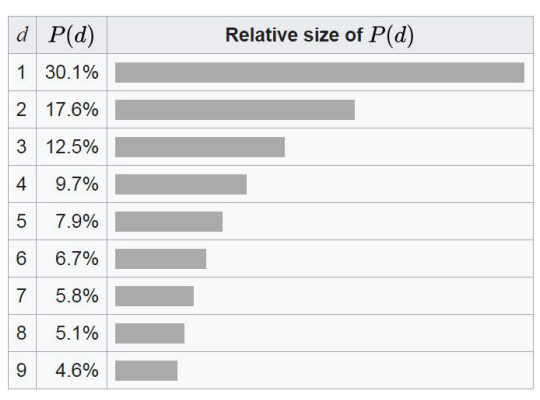
A set of decimal numbers is said to satisfy Benford’s law if the leading digit \(d\) \((d ∈ \{1, …, 9\})\) occurs with probability:
$$P(d)=\log _{ 10 }{ \left( 1+\frac { 1 }{ d } \right) } .$$
The leading digits in such a set thus have the following distribution:
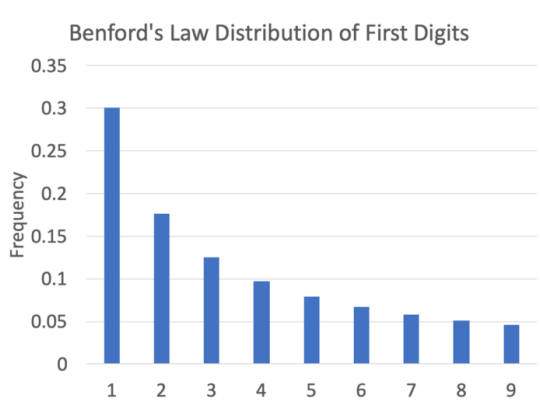
A more conventional form of graphical representation of this law is in the form of a histogram or bar chart:
An extension of Benford’s law predicts the distribution of first digits in other bases besides decimal. Benford’s law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.
Traditionally, Benford’s law is applicable to data sets from natural and accounting origins. However, there are some indications that it might also be applicable to data generated as the consequence of mathematical operations (Fibonacci numbers is a good example). This law applies very well to numbers representing several orders of magnitude: prices, populations, lengths, etc.
Recently this law has found wide application in forensic accounting for fraud detection, in economics for pricing research and macroeconomic data analysis, for scientific fraud detection and many more. Its application for election data analysis is debatable, though the second-digit Benford’s law test for identifying irregularities and fraud in election results in a number of countries was recently made.
To test the hypothesis of compliance of the input data set with Benford’s law our online Benford’s law calculator uses the chi-square goodness-of-fit test. Note that it has low statistical power when used with small samples. To test the significance of the above compliance the P-value is then calculated.
Related calculators
Check out our other statistics calculators such as Chi Square Calculator or P-value Calculator.