Cross Product Calculator

This online Cross Product Calculator finds the cross product of two vectors in three-dimensional space. You can paste the input vectors components copied from a spreadsheet or csv-file or enter manually using comma, space or enter as separators. The components of the resultant vector can be space or comma separated.

c = a × b

Cross Product of Vectors

In mathematics, the cross product or vector product is a binary operation on two vectors in three-dimensional space. Given two linearly independent vectors a and b, the cross product, a × b (read “a cross b“), is a vector that is perpendicular to both a and b, and thus normal to the plane containing them.

The most important properties of cross product include the following.
• In the case when two vectors are collinear or if either one has zero length, then their cross product is zero.
• The cross product is distributive over addition (that is, a × (b + c) = a × b + a × c).
• The cross product is anticommutative (that is, a × b = − b × a).

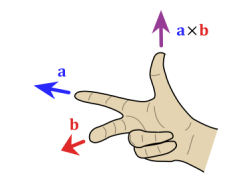
The cross product a × b is defined as a vector c that is perpendicular (orthogonal) to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span. According to the right-hand rule one points the forefinger of the right hand in the direction of a and the middle finger in the direction of b. Then, the vector c is coming out of the thumb.

The cross product of two vectors is defined by the formula:

where:
• θ is the angle between the vectors a and b in the plane containing them,
• |a| and |b| represent the magnitudes of the vectors,
• n is a unit vector perpendicular to the plane containing a and b, in the direction given by the right-hand rule.

As is well known from linear algebra each vector in three-dimensional space can be defined as the sum of three orthogonal components parallel to the standard basis vectors. So, in a right hand coordinate system each vector can be represented by three coordinates. For example, a = {a_x, a_y, a_z}.

It is easy to obtain expressions for coordinates of the vector c given the coordinates of vectors a and b:

We obtained fairly simple formulas for the coordinates of the resultant vector. However, in order not to get confused in the calculations, the easiest way is to use our cross product calculator.

Related calculators

Check out our other algebra calculators such as Dot Product Calculator or Point Slope Form Calculator.