This online Capacitance Calculator allows you to calculate the capacitance of some simple objects. To get the result, you first select the object, then enter the known values of the object’s parameters into the input fields of this calculator and click the ‘Calculate’ button.
What is Capacitance
In physics, capacitance is defined as the measure of an object’s ability to store electrical charge. It is symbolized by the letter \(C\) and is quantified by the ratio of change in charge stored on an object (or system) to the change in potential or potential difference (voltage) across it in response to the change in charge:
$$C = \frac {\Delta Q}{\Delta V},$$
where \(\Delta Q\) is the change in charge, \(\Delta V\) is the change in potential (voltage).
The SI unit of capacitance is the farad (F), named after Michael Faraday. Dimension: M-1·L-2·T4·I2.
An important practical application of this concept is associated with a device called a capacitor. A capacitor is an elementary linear electronic component designed to add capacitance to an electrical circuit.
Capacitors, electronic components specifically designed to store electrical charge, have widespread use in numerous electrical and electronic systems. They come in various shapes, sizes, and materials to suit different applications. Some common applications include: energy storage systems, filtering and coupling circuits, timing circuits and oscillators, power factor correction circuits.
Two Types of Capacitance
There are two types of capacitance: self capacitance and mutual capacitance. Self capacitance refers to the inherent capacitance possessed by a single object that can be electrically charged. In this case the electric potential is measured between the object and ground. The self capacitance depends on the size, shape, and material properties of the object and the surrounding medium.
Mutual capacitance arises when two conductive objects or surfaces are placed in relative proximity to each other. In this scenario, the capacitance is influenced by the overlapping electric fields between the objects. The mutual capacitance value depends on several factors, such as the distance between the objects, the size and shape of the conductors, and the property of the medium between them.
The capacitance of an object greatly depends on the properties of the surrounding medium. This property is described by the concept of permittivity. Permittivity, denoted by the symbol \(\varepsilon\), quantifies a material’s ability to permit the formation of an electric field within it. The higher the permittivity of a medium, the greater the capacitance of a capacitor constructed with that material.
The vacuum permittivity is a constant, denoted by the letter \(\varepsilon_0 \approx \) 8.854188×10-12 F/m. It is the vacuum permittivity that is used as the default value in our Capacitance Calculator. If you need to make a calculation for a particular material, then you need to insert the permittivity value of that material in the appropriate field of the calculator. The table below shows the permittivity values of some materials.
Examples of Сalculating Сapacitance
Сonducting sphere
As a first example, consider a solitary conducting sphere of radius \(R\) in vacuum. Obviously, in this case we are dealing with self capacitance.
Then, applying the above general formula, we must keep in mind that \(\Delta Q\) is the electric charge that we have added to the surface of the sphere, and \(\Delta V\) is the change in potential on the surface of the sphere after adding the charge. If we recall that initially the electric potential on the surface was equal to zero (as well as at infinity), then it is easy to understand that \(\Delta V\) is the potential difference on the sphere and at infinity.
In the general case, the potential on the surface of any isolated object can be calculated by integrating the charge density over its surface and taking into account Coulomb’s law. In the case of a sphere, we use symmetry considerations and arrive at the following simple result:
$$C = 4 \pi \varepsilon_0 R.$$
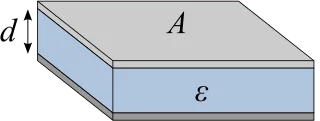
Parallel-plate capacitor
As a second example, consider the capacitance of a flat capacitor consisting of two parallel conducting plates with area \(A\) each separated by a distance \(d\).
If \(d\) is small enough with respect to the linear dimensions of the plates, then a uniform electric field is established between the plates with a high degree of accuracy. Further, instead of applying the Coulomb’s law and integration, one can use the Gauss’s law and symmetry considerations. As a result, it is easy to come to the following result:
$$C = \varepsilon \frac{A}{d},$$
where \(\varepsilon\) is the permittivity of an insulator between the capacitor plates.
Сalculating Сapacitance of Objects
The calculation of capacitance is not fundamentally difficult if the geometry of the conductors and the dielectric properties of the medium between the conductors are known. Although technically the process of integration in the case of complex objects and surfaces can be very laborious.
The capacitance formulas for some simple objects that you can select from our Capacitance Calculator are listed for reference in the table below. The data and figures it contains are from Wikipedia.
Indeed, to calculate the capacitance of a particular object, it is much more convenient to use our online calculator. Using it can save you time and effort compared to manual calculations, especially for more complex objects or shapes.
Capacitance of Simple Objects
$$C = \frac{\varepsilon A}{d}$$
$$C = \frac{2 \pi \varepsilon L}{ln(R_2/R_1)}$$
$$C = \frac{2 \pi \varepsilon L}{ arcosh \left ( \frac{R_1^2+R_2^2-d^2}{2 R_1 R_2} \right )}$$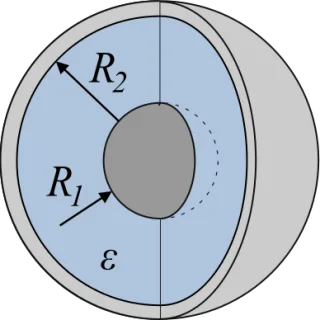
$$C = \frac{4 \pi \varepsilon R_1 R_2}{R_2 \ – \ R_1}$$
$$C = \frac{\pi \varepsilon L}{ arcosh \left ( \frac{d}{2a} \right )}$$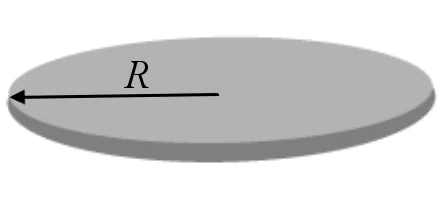
$$C = 8 \varepsilon R$$
$$C = 4 \pi \varepsilon R$$Related calculators
Check out our other physics calculators such as Capacitors in Series Calculator or Capacitive Reactance Calculator.