This online Center of Mass Calculator calculates the coordinates of the center of mass for an arbitrary number of point masses in the case of one-dimensional, two-dimensional or three-dimensional space. To get the result, you first select the space dimension. Then enter the known values of masses and coordinates into the input fields of this calculator and click the ‘Calculate’ button. To add or delete a mass you may click the “+” symbol or the “–” symbol respectively.
Center of Mass Formula
In physics, the center of mass of a distribution of mass in space (a.k.a the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point, the application of forces to which, causes a linear acceleration without an angular acceleration.
Calculations in mechanics are often simplified if they are formulated with respect to the center of mass. The center of mass can be thought of as a hypothetical point at which it can be assumed that the entire mass of an object is concentrated. This makes it easier to visualize the motion of that object. In other words, the center of mass is a hypothetical particle equivalent to a given object to which Newton’s laws of motion can be applied.
The terms “center of mass” and “center of gravity” are used as synonyms in the case of a uniform gravitational field. Both terms refer to a unique point in an object or system that can be used to describe the system’s response to external forces and torques.
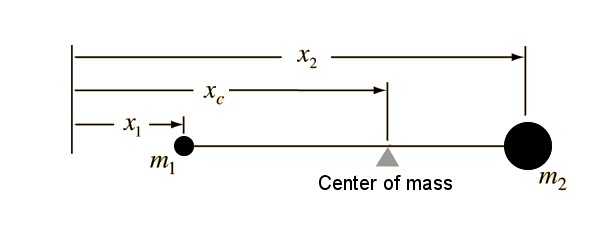
In the case of a plane and two masses, this is like balancing a seesaw around a pivot point with respect to the torques produced. For two masses we have the following center of mass formula:
$$x_{c}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}},$$
where
\(m_{i}\) is the mass of particle \(i\),
\(x_{i}\) is the coordinate of particle \(i\),
\(x_{c}\) is the center of mass coordinate.
If you are making measurements from the center of mass point for such a two-mass system, then the center of mass condition can be expressed as:
$$m_1 \ | x_1 | = m_2 \ | x_2 |.$$
The center of mass lies on the line connecting the two masses.
In the case of an arbitrary number of particles, the formula for the center of mass is generalized as follows:
$$x_{c}=\frac{m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}+…}{m_{1}+m_{2}+m_{3}+…}.$$
In the case of multidimensional space, this formula also applies to the \(y\) and \(z\) coordinates.
With our Center of Mass Calculator you can easily compute the coordinates of the center of mass for an arbitrary number of point masses in one-dimensional, two-dimensional or three-dimensional space.
Related calculators
Check out our other physics calculators such as Torque Calculator or Work Calculator.