This online Centroid Calculator allows you to find the centroid coordinates for a triangle, an N-sided polygon, or an arbitrary set of N points in the plane. To get the result, you first select the shape, then enter the known values of coordinates into the input fields of this calculator and click the ‘Calculate’ button.
Centroid Formula
In mathematics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points of the figure.
If a plane figure is a real object with a uniformly distributed mass, then the centroid coincides with the center of mass of this object. The concept of centroid can also be extended to three-dimensional objects.
The geometric centroid of a convex object always lies inside the object itself. A non-convex object can have a centroid that is outside of the object itself.
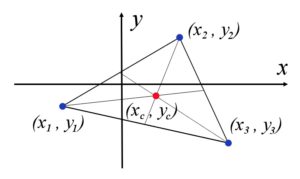
The centroid of a triangle is the intersection point of its medians. Recall that the median of a triangle is the line that connects each vertex to the midpoint of the opposite side. It can be shown that all medians of a triangle intersect at one point. The centroid divides each of the medians in a ratio of 2:1, that is, it is located 1/3 of the distance from each side to the opposite vertex.
In the general case of a non-self-intersecting closed polygon given by \(n\) vertices with coordinates \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), …, \((x_{n}, y_{n})\), the coordinates of the corresponding centroid \((x_{c}, y_{c})\) are defined by the following formulas:
$$x_{c}=\frac{x_{1}+x_{2}+…+x_{n}}{n},$$
$$y_{c}=\frac{y_{1}+y_{2}+…+y_{n}}{n}.$$
The same formulas also apply to calculate the coordinates of the centroid for an arbitrary system of \(n\) points in the plane.
With our Centroid Calculator you can easily calculate the centroid coordinates for a triangle, an arbitrary \(n\)-sided polygon or a system of \(n\) points in the plane.
Related calculators
Check out our other geometry calculators such as Ellipse Calculator or Rhombus Area Calculator.