This online Linear Interpolation Calculator allows you to find the coordinates of an arbitrary point lying on a straight line connecting two known points in the plane. You have to specify the coordinates of the two known points and x- or y- coordinate of the point of interest. After clicking the ‘Calculate’ button you will get the second coordinate of the point of interest as well as the interpolation line parameters.
y = ax + b
Linear Interpolation Formula
Interpolation is a method for estimating the value of a function between any two known values. Linear interpolation assumes that there is a linear relationship between the coordinates of points in the interval between two known points. In the case of a two-dimensional plane, this dependence is expressed by the following formula:
$$y = ax + b,$$
where \(a\) and \(b\) are constants.
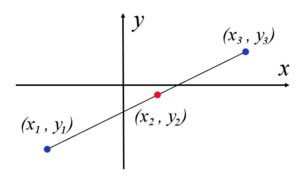
For a value \(x\) within the interval \((x_{1},x_{3})\), the value \(y\) of a point that lays on a straight line passing through the points \((x_{1},y_{1})\) and \((x_{3},y_{3})\) can be found from the equation of slopes:
$${\frac {y-y_{1}}{x-x_{1}}}={\frac {y_{3}-y_{1}}{x_{3}-x_{1}}},$$
which can be derived geometrically from the figure.
Solving this equation for \(y\) we can get:
$$y=y_{1}+(x-x_{1}){\frac {y_{3}-y_{1}}{x_{3}-x_{1}}},$$
which is the formula for linear interpolation in the interval \((x_{3},x_{1})\). It is important to note that the value \(x\) can also be chosen outside this interval. In this case we get a similar formula that can be used for linear extrapolation. So our linear interpolation calculator that uses this formula can also be used as a linear extrapolation calculator.
Comparing this formula with the above general formula for a linear function, we can easily find expressions for the parameters of this function:
$$a = \frac {y_{3}-y_{1}}{x_{3}-x_{1}},$$
$$b = y_{1}-x_{1}{\frac {y_{3}-y_{1}}{x_{3}-x_{1}}}.$$
Linear interpolation is useful while searching for a value between given data points. But it is important to remember that linear interpolation is not accurate for non-linear data. If the points in the dataset vary in a highly non-linear fashion, then linear interpolation may give poor estimates. In this case, the accuracy of estimates can be increased by reducing the intervals between known points.
Related calculators
Check out our other math calculators such as Midpoint Calculator or Perpendicular Line Calculator.