Moment of Inertia Calculator

This online Moment of Inertia Calculator allows you to calculate the moment of inertia of objects of different shapes. To get the result, you first select the shape of the object. Then enter the known values of masses and distances into the input fields of this calculator and click the ‘Calculate’ button.

What is Moment of Inertia in Physics?

In physics, the moment of inertia (a.k.a the mass moment of inertia, angular mass, second moment of mass, or rotational inertia) is a measure of an object’s resistance to rotational motion. It is similar to mass in case of linear motion, in that it represents an object’s inertia or resistance to change in its state of motion. Just as a larger mass requires a greater force to move it, an object with a larger moment of inertia requires a greater torque to rotate it.

The moment of inertia of an object depends not only on its mass, but also on how that mass is distributed about its axis of rotation. In general, objects with more mass located farther away from the axis of rotation have a larger moment of inertia than objects with less mass or mass closer to the axis of rotation.

The concept of moment of inertia has many important applications in physics and engineering. It is crucial for understanding rotational motion and the behavior of objects under torque. For example, it can be used to calculate the angular acceleration of an object subjected to a certain torque, or to determine the speed and direction of an object after a collision.

In addition, moment of inertia plays a key role in the design of many mechanical systems, such as engines, turbines, and flywheels. By optimizing the moment of inertia of these systems, engineers can improve their efficiency, stability, and overall performance.

Moment of Inertia Formulas

The formula for the moment of inertia of a point mass relative to an axis of rotation is:

$$I = mr^2,$$

where \(I\) is the moment of inertia, \(m\) is the mass of the point, and \(r\) is the distance of the point from the axis of rotation.

For a system of \(n\) discrete masses, the moment of inertia is calculated by summing up the products of each mass and the square of its distance from the axis of rotation. Mathematically, this can be expressed as:

$$I = \sum_{i=1}^{n}m_{i}r_{i}^{2},$$

where \(I\) is the moment of inertia, \(m_i\) is the mass of the \(i\)-th particle, and \(r_i\) is the distance of the \(i\)-th particle from the axis of rotation.

For objects with a spatially continuous mass distribution, the moment of inertia can be calculated using the integration process. This method involves dividing the object into infinitesimally small elements and calculating the contribution of each element to the moment of inertia.

The formula for calculating the moment of inertia of a solid object can thus be expressed as:

$$I = \int r^2 dm,$$

where \(I\) is the moment of inertia, \(r\) is the distance from the axis of rotation to the element of mass \(dm\), and the integral symbol (\(\int\)) represents the process of integration.

Moment of inertia has dimension M·L². The SI unit of moment of inertia is kilogram meter squared (kg·m²). Imperial or US units are pound foot second squared lb·ft·s² or pound foot squared lb·ft².

Example of a solid cylinder

To use the above general formula for the moment of inertia of a homogeneous object (i.e., an object with a constant mass density), you must first determine the mass density of the object, which is the mass per unit volume or unit area. For example, the mass density of a uniform solid cylinder can be expressed as:

$$\rho = m/V = m/ \pi R^2 H,$$

where \(\rho\) is the mass density, \(m\) is the total mass of the cylinder, \(R\) is the radius of the cylinder, and \(H\) is its height.

Once the mass density is known, you can integrate over the entire object to calculate its moment of inertia. So the moment of inertia of a solid cylinder about the axis of rotation passing through its center parallel to its height can be calculated as follows:

$$I = \int r^2 dm = \rho \int_{0}^{H} \int_{0}^{2\pi} \int_{0}^{R} r^3 dr d\theta dh = 2 \pi \rho H \int_{0}^{R} r^3 dr = (1/2)mR^2,$$

where the integral is performed over the volume of the cylinder, and the result is simplified using basic calculus techniques.

Theorems of moment of inertia

Worth emphasizing that the choice of the axis of rotation is very important, since the final value of the moment of inertia usually strongly depends on this. Usually, various reference sources indicate the values of moments of inertia of objects relative to the axis of rotation passing through the geometric center of the object, which usually coincides with its center of mass.

If you need to know the moment of inertia of a rigid body relative to another axis that is parallel to the one passing through the center of mass of the body, you can use the parallel axis theorem. The formula expressing this theorem can be written as:

$$I = I_{cm} + md^2,$$

where \(I\) is the moment of inertia of the body about the desired axis, \(I_{cm}\) is the moment of inertia of the body about an axis that passes through its center of mass and is parallel to the desired axis, \(m\) is the total mass of the body, and \(d\) is the perpendicular distance between the two axes.

In other words, to calculate the moment of inertia of a body about a parallel axis, you first calculate the moment of inertia about an axis that passes through the body’s center of mass, and then add a term that depends on the mass of the body and the distance between the two axes.

In some cases, when calculating the moment of inertia of a body, the perpendicular axis theorem can be extremely useful. The perpendicular axis theorem is a formula that allows us to calculate the moment of inertia of a planar body (i.e., a body that lies entirely in a single plane) about an axis that is perpendicular to that plane. This formula can be expressed in the following form:

$$I_z = I_x + I_y,$$

where \(I_z\) is the moment of inertia of the body about an axis perpendicular to the plane of the body, and \(I_x\) and \(I_y\) are the moments of inertia of the body about two perpendicular axes that lie in the plane of the body. Note that all three perpendicular axes \(x\), \(y\), and \(z\) must meet at the origin \(O\).

That is, to calculate the moment of inertia of a planar body about an axis perpendicular to the plane, you can first calculate the moments of inertia of the body about two perpendicular axes that lie in the plane, and then add those two moments of inertia together.

Moment of Inertia of Simple Objects

The process of integration when calculating the moment of inertia can be quite sophisticated for more complex shapes, but it follows the same general pattern of dividing the object into small elements and integrating their contributions to the moment of inertia.

The moments of inertia of some simple homogeneous objects that you can select from our Moment of Inertia Calculator are listed for reference in the table below. The data and figures it contains are from Wikipedia.

Indeed, to calculate the moment of inertia of a particular object, it is much more convenient to use our online calculator. Using it can save you time and effort compared to manual calculations, especially for more complex objects or shapes. It can also help you to better understand the relationship between an object’s mass, shape, and moment of inertia.

Table of Moments of Inertia

Ball. Solid sphere (ball) of radius \(r\) and mass \(m\) with axis of rotation going through its center.

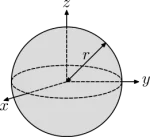$$I_{center} = \frac{2}{5}mr^{2}$$

Circular hoop. Thin circular hoop of radius \(r\) and mass \(m\) with three axes of rotation going through its center: parallel to the \(x\), \(y\) and \(z\) axes.

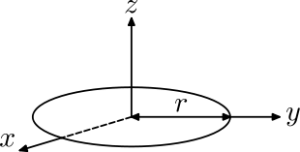$$I_{x} = I_{y} = \frac{1}{2}mr^{2}$$ $$I_{z} = mr^{2}$$

Cylinder. Solid cylinder of radius \(r\), height \(h\) and mass \(m\) with three axes of rotation going through its center: parallel to \(x\), \(y\) and \(z\) axes.

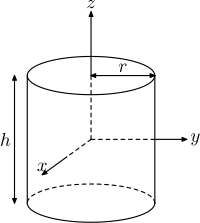$$I_{x} = I_{y} = \frac{1}{12}m(3r^{2}+h^{2})$$ $$I_{z} = \frac{1}{2}mr^{2}$$

Cylindrical tube. Cylindrical tube of inner radius \(r_1\), outer radius \(r_2\), height \(h\) and mass \(m\) with three axes of rotation going through its center: parallel to \(x\), \(y\) and \(z\) axes.

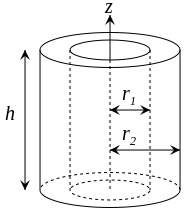$$I_{x,y} = \frac{1}{12}m(3(r_1^{2}+r_2^{2})+h^{2})$$ $$I_{z} = \frac{1}{2}m(r_1^{2}+r_2^{2})$$

Disk. Thin solid disk of radius \(r\) and mass \(m\) with three axes of rotation going through its center: parallel to the \(x\), \(y\) and \(z\) axes.

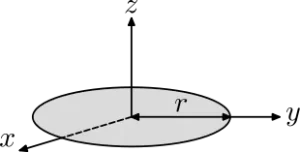$$I_{x} = I_{y} = \frac{1}{4}mr^{2}$$ $$I_{z} = \frac{1}{2}mr^{2}$$

Ellipsoid. Solid ellipsoid of semiaxes \(a\), \(b\), \(c\), and mass \(m\) with three axes of rotation going through its center: parallel to the \(a\), \(b\), or \(c\) semiaxes.

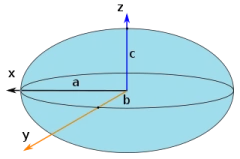$$I_{a} = \frac{1}{5}m(b^{2}+c^{2})$$ $$I_{b} = \frac{1}{5}m(a^{2}+c^{2})$$ $$I_{c} = \frac{1}{5}m(a^{2}+b^{2})$$

Hollow cone. Hollow right circular cone of radius \(r\), height \(h\), and mass \(m\) with three axes of rotation going through its center: parallel to the \(x\), \(y\) and \(z\) axes.

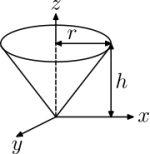$$I_{x} = I_{y} = \frac{1}{4}m(r^{2}+2h^{2})$$ $$I_{z} = \frac{1}{2}mr^{2}$$

Point mass. Point mass \(m\) at a distance \(r\) from the axis of rotation.

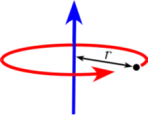$$I = mr^{2}$$

Rectangular plate. Thin rectangular plate of length \(l\), width \(w\), and mass \(m\) with axis of rotation going through its center, perpendicular to the plane of the plate.

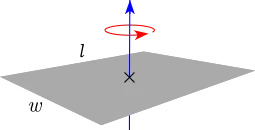$$I_{⊥center} = \frac{1}{12}m(l^{2}+w^{2})$$

Rod. Thin rod of length \(L\) and mass \(m\) with two axes of rotation perpendicular to the rod: about its center and about its end.

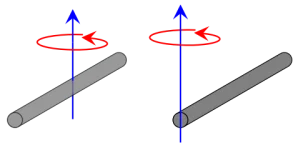$$I_{center} = \frac{1}{12}mL^{2}, \ I_{end} = \frac{1}{3}mL^{2}$$

Solid cone. Solid right circular cone of radius \(r\), height \(h\), and mass \(m\) with three axes of rotation passing through its center: parallel to the \(x\), \(y\) and \(z\) axes.

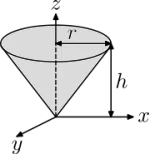$$I_{x} = I_{y} = \frac{3}{20}m(r^{2}+4h^{2})$$ $$I_{z} = \frac{3}{10}mr^{2}$$

Solid cuboid. Solid cuboid of length \(l\), width \(w\), height \(h\) and mass \(m\) with three axes of rotation going through its center: parallel to the length \(l\), width \(w\) and height \(h\).

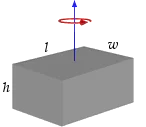$$I_{l} = \frac{1}{12}m(w^{2}+h^{2})$$ $$I_{w} = \frac{1}{12}m(l^{2}+h^{2})$$ $$I_{h} = \frac{1}{12}m(l^{2}+w^{2})$$

Sphere. Hollow sphere of radius \(r\) and mass \(m\) with axis of rotation going through its center.

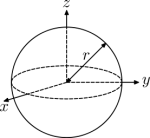$$I_{center} = \frac{2}{3}mr^{2}$$

Spherical shell. Spherical shell of inner radius \(r_1\), outer radius \(r_2\), and mass \(m\) with axis of rotation going through its center.

$$I_{center} = \frac{2}{5}m \left ( \frac{r_2^5-r_1^5}{r_2^3-r_1^3} \right )$$

Tetrahedron. Regular tetrahedron (solid and hollow) of side \(s\) and mass \(m\) with axis of rotation going through a tetrahedron’s vertex and its center.

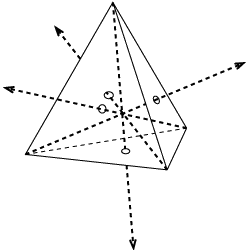$$I_{solid} = \frac{1}{20}ms^{2}$$ $$I_{hollow} = \frac{1}{12}ms^{2}$$

Torus. Torus with minor radius \(a\), major radius \(b\) and mass \(m\) with axes of rotation going through its center: perpendicular to the major diameter and parallel to the major diameter.

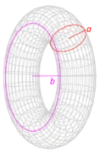$$I_{⊥torus} = \frac{1}{4}m(3a^{2}+4b^{2})$$ $$I_{||torus} = \frac{1}{8}m(5a^{2}+4b^{2})$$

Two point masses. Two point masses \(m_1\) and \(m_2\), separated by a distance \(x\) with axis of rotation going through the center of mass and perpendicular to the plane of motion of the masses.

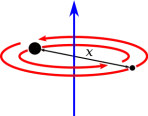$$I = \frac{m_{1}m_{2}}{m_{1}+m_{2}}x^{2}$$

Uniform annulus. Uniform annulus (disk with a concentric hole) of mass \(m\), inner radius \(r_1\) and outer radius \(r_2\) with three axes of rotation going through its center: parallel to the \(x\), \(y\) and \(z\) axes.

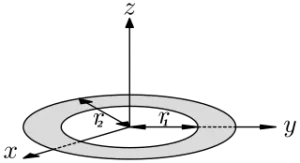$$I_{x} = I_{y} = \frac{1}{4}m(r_1^{2}+r_2^{2})$$ $$I_{z} = \frac{1}{2}m(r_1^{2}+r_2^{2})$$

Related calculators

Check out our other physics calculators such as Center of Mass Calculator or Torque Calculator.