Prime Factorization Calculator

This online Prime Factorization Calculator finds all prime factors of a given integer number between 2 and 2⁵³ – 1 = 9007199254740991. Prime decomposition of the number is presented in exponential form. Enter the number in the input field of the calculator and click the ‘Calculate’ button to get the result.

What is Prime Factorization?

Prime factorization (or prime decomposition) is the process of integer factorization when a composite integer number is decomposed into a product of smaller integers which are all prime numbers. According to the fundamental theorem of arithmetic, every positive integer has a unique prime factorization.

In mathematics, factors are numbers that, when multiplied by each other, produce a given number. A prime number is such a number that is only divisible by the number 1 and itself. Thus, prime factorization of a number is the process of getting all the prime numbers that, when multiplied by each other, give that number. Or, in other words, writing a number as a product of primes.

Let’s consider some examples.

What is the prime factorization of 48? 48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3.

What is the prime factorization of 450? 450 = 2 × 3 × 3 × 5 × 5 = 2 × 3² × 5².

What is the prime factorization of 2310? 2310 = 2 × 3 × 5 × 7 × 11.

Prime factorization of numbers has several practical applications. In number theory it is often used to study the properties and behavior of numbers. In cryptography the RSA algorithm, a widely used method for secure data transmission, is based on the fact that the factorization of large composite numbers is very difficult. Prime factorization is used in image and video compression algorithms. It is also used in error correction algorithms and a number of other areas.

Prime Factorization Methods

There are many methods of prime factorization of a number. The most common methods are as follows.

Trial Division

The simplest method of finding prime factors is using a trial division (or direct search factorization) algorithm. It consists of searching for prime factors of a number by systematically performing trial divisions using a sequence of increasing prime numbers. This “brute force” method is not efficient enough and can only be used with relatively small numbers.

The trial division algorithm generally has the following steps:

1) Take the first prime number, 2, as the trial divisor. Consider the original number as the dividend.

2) If the trial divisor equals to the dividend, then write the used trial divisor into the list of prime factors of the original number and quit. If not, then try to divide the dividend by the trial divisor without a remainder.

3) If such a division is possible, write the used trial divisor into the list of prime factors of the original number. Consider the result of the division as the new dividend and go to step 2.

4) If such division is not possible, take the next largest prime number as the new trial divisor and go to step 2.

A slightly modified trial division algorithm is used in our Prime Factorization Calculator.

Example of Trial Division

Consider the decomposition of the number 765 into prime factors and apply the algorithm described above.

1) Let’s start with the first prime number 2 as a trial divisor.
2) We see that our number is greater than 2. Therefore, we will try to divide it by 2 without a remainder.
3) Being odd, this number is not divisible by 2 without a remainder.
4) Therefore, we move on to consider the next largest prime number (this is the number 3) and proceed to step 2 of our algorithm.

2) We see that our number is greater than 3. Therefore, we will try to divide it by 3. Our original number is divisible by 3 without a remainder. This is easy to check because the sum of the digits of this number 7+6+5=18 is divisible by 3.
3) We write the number 3 in the list of prime factors (LFP) of our number: LPF = 3. We will consider the result of division 765/3 = 255 as a new dividend and move on to step 2 of our algorithm.

2) We see that our new dividend is greater than 3. Therefore, we will try to divide it by 3. Our dividend is divisible by 3 without a remainder, since the sum of the digits of this number 2+5+5=12 is divisible by 3.
3) We write the number 3 in the list of prime factors of our initial number: LPF = 3, 3. We will consider the result of division 255/3 = 85 as a new dividend and go back to step 2 of our algorithm.

2) We see that the new dividend is greater than 3. Therefore, we will again try to divide it by 3.
3) However, the number 85 is not divisible by 3 without a remainder.
4) Therefore, we move on to consider the next largest prime number (this is the number 5) and proceed to step 2 of our algorithm.

2) We see that our dividend 85 is greater than 5. So let’s try to divide it by 5. It is obviously divisible by 5 without a remainder, since the number 85 ends with 5.
3) We write the number 5 in the list of prime factors of our number: LPF = 3, 3, 5. We will consider the result of division 85/5 = 17 as a new dividend and go back to step 2 of our algorithm.

2) It is easy to check that the next prime numbers less than our new dividend 17, namely the numbers 7, 11, 13, do not divide it without a remainder. But the next prime number 17 is equal to our dividend. Therefore, we write it down in the list of prime factors of our number: LPF = 3, 3, 5, 17 and complete the calculations.

Factor Trees

This visual method of prime decomposition involves building a factor tree. The creation of a factor tree consists of splitting a composite number into factors of that number until all numbers are prime.

We start with the given number at the top of the tree. Then, we draw two branches towards two factors of that number. We repeat the process for the numbers at the end of each branch until each “leaf” is a prime number.

If from the very beginning we choose only prime numbers as factors, we will actually come to the graphical representation of the above trial division algorithm. In the example below, we find the prime factors of the number 765.

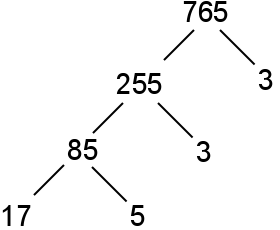
Thus, as we can see, the prime factorization of 765 gives us again the result: 765 = 3² × 5 × 17.

Prime factorizations of some common numbers

Related calculators

Check out our other math calculators such as Factoring Calculator or Decimal To Fraction Converter.