Vector Addition Calculator

---

This online Vector Addition Calculator finds the sum of any number of 2D or 3D vectors represented as sets of Cartesian coordinates. To get the result just enter the known values of the vectors coordinates into the input fields of this calculator and click the ‘Calculate’ button. To add or delete a vector you may click the “+” symbol or the “–” symbol respectively.

---

Dimensions: 2D3D

---

Vectors

x₁:

y₁:

Vector sum

x_s:

y_s:

Vectors

x₁:

y₁:

z₁:

Vector sum

x_s:

y_s:

z_s:

---

What is a Vector

Vectors are fundamental mathematical objects that play an important role in various scientific disciplines, including physics and engineering. They provide a concise and efficient way of representing quantities that have both magnitude and direction.

In mathematics, a vector is an object consisting of two main components: magnitude (or length) and direction in space. In diagrams and graphs, vectors are usually depicted with arrows and denoted by bold letters or letters with arrows, such as \(\textbf{V}\) or \(\overrightarrow{V}\).

Any vector can be uniquely defined by its projections on the coordinate axes in the space in which it acts. In other words, a vector can be algebraically defined by a set of numbers that can be considered as its components. For example, in a three-dimensional Cartesian coordinate system, any vector can be represented as follows:

$$\overrightarrow{V} = \{ V_x, V_y, V_z \}.$$

Vector Addition

Adding vectors is a mathematical operation that takes into account both their magnitudes and directions.

When vectors are defined graphically, it is most natural to use geometrical methods of addition. The geometrical method of vector addition, also known as the graphical method, is an approach to combining vectors visually using geometric constructions. It involves drawing vectors as directed line segments and using geometric operations.

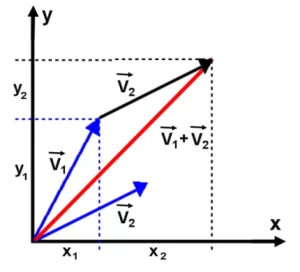
The simplest and most obvious is the head-to-tail method. In the head-to-tail method, vectors are represented as arrows or directed line segments. To add two vectors \(\overrightarrow{V_{1}}\) and \(\overrightarrow{V_{2}}\), the tail of vector \(\overrightarrow{V_{2}}\) is placed at the head of vector \(\overrightarrow{V_{1}}\). The resultant vector, denoted as \(\overrightarrow{V_{s}}\) = \(\overrightarrow{V_{1}}\) + \(\overrightarrow{V_{2}}\), is then drawn from the tail of vector \(\overrightarrow{V_{1}}\) to the head of vector \(\overrightarrow{V_{2}}\). The length and direction of vector \(\overrightarrow{V_{s}}\) represent the magnitude and direction of the resultant vector.

Another method which is called the parallelogram method is essentially reduced to the same head-to-tail method.

The algebraic method of vector addition consists of adding the corresponding components of the vectors involved. For instance, if we have two vectors \(\overrightarrow{V_{1}}\) and \(\overrightarrow{V_{2}}\) in 2D space, their sum, denoted as \(\overrightarrow{V_{s}}\), is computed as follows:

$$\overrightarrow{V_{s}} = \{ x_s, y_s\} = \overrightarrow{V_{1}} + \overrightarrow{V_{2}} = \{ x_1+x_2, y_1+y_2 \},$$

where \(x_i\) and \(y_i\) are x- and y- components of the vector \(\overrightarrow{V_{i}}\).

This formula can be generalized to any number of vectors and to spaces of different dimensions. Our online Vector Addition Calculator is able to easily calculate the sum of an arbitrary number of vectors defined by their Cartesian components in 2D or 3D spaces.

Properties of Vector Addition

Vector addition has the following basic algebraic properties.

• Commutative Property: The order in which vectors are added does not affect the result. In other words, \(\overrightarrow{V_{1}}\) + \(\overrightarrow{V_{2}}\) = \(\overrightarrow{V_{2}}\) + \(\overrightarrow{V_{1}}\).

• Associative Property: The grouping of vectors being added does not alter the outcome. For three vectors \(\overrightarrow{V_{1}}\), \(\overrightarrow{V_{2}}\) and \(\overrightarrow{V_{3}}\),   (\(\overrightarrow{V_{1}}\) + \(\overrightarrow{V_{2}}\)) + \(\overrightarrow{V_{3}}\) = \(\overrightarrow{V_{1}}\) + (\(\overrightarrow{V_{2}}\) + \(\overrightarrow{V_{3}}\)).

• Identity Property: There exists a unique vector called the zero vector, denoted as \(\overrightarrow{0}\), which does not change the magnitude or direction of other vectors when added. For any vector \(\overrightarrow{V}\),   \(\overrightarrow{V}\) + \(\overrightarrow{0}\) = \(\overrightarrow{V}\).

• Inverse Property: For every vector \(\overrightarrow{V}\), there exists a unique vector called the additive inverse or negative vector, denoted as –\(\overrightarrow{V}\), such that \(\overrightarrow{V}\) + (-\(\overrightarrow{V}\)) = \(\overrightarrow{0}\).

• Distributive Property: Vector addition follows the distributive property with scalar multiplication. For a scalar \(c\) and vectors \(\overrightarrow{V_1}\) and \(\overrightarrow{V_2}\), \(c\)(\(\overrightarrow{V_1}\) + \(\overrightarrow{V_2}\)) is equal to \(c\)\(\overrightarrow{V_1}\) + \(c\)\(\overrightarrow{V_2}\). So the scalar multiplication can be distributed over vector addition.