This online Vector Projection Calculator finds the orthogonal projection of vector a onto the vector b defined in a space of arbitrary dimension. You can paste to the respective fields of the calculator the vectors components copied from a spreadsheet or csv-file or input manually using comma, space or enter as separators.
What is a Vector Projection
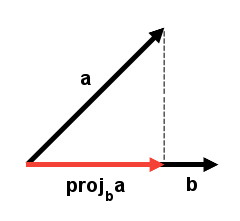
In mathematics, the projection of vector \(a\) onto a nonzero vector \(b\) is a new vector (commonly referred to as \(proj_b a\)) that lies along the direction of \(b\), representing how much of \(a\) points in the direction of \(b\).
This concept is closely related to the idea of “shadowing” one vector onto another. If you were to shine a light perpendicular to vector \(b\), the shadow that vector \(a\) casts onto \(b\) is its projection. This projection helps to estimate the influence of \(a\) in the direction of \(b\).
Vector projection is widely used, for example, in physics for analyzing motion, calculating work done by a force, resolving forces, and understanding energy and power in dynamic systems. By projecting one vector onto another, physicists can isolate the effective part of a force or velocity that actually influences motion or energy transfer.
Vector Projection Formula
The orthogonal vector projection of \(a\) onto \(b\) is given by the following formula:
$$proj_b a = \left ( \frac{a\cdot b}{\left\| b\right\|^{2}}\right ) b$$
where
• \(a\cdot b\) is the dot product of vectors \(a\) and \(b\),
• \(\left\| b\right\|^{2}\) is the square of the length of \(b\).
The following key properties of vector projection follow directly from the above formula:
- The projection vector always points in the same or opposite direction as \(b\), depending on the sign of the dot product.
- If vectors \(a\) and \(b\) are orthogonal (perpendicular), the projection is the zero vector.
We would like to emphasize that our Vector Projection Calculator is designed to work with vectors defined in a vector space of arbitrary dimension (i.e. having an arbitrary number of components).
Related calculators
Check out our other algebra calculators such as Vector Addition Calculator or Vector Subtraction Calculator.