This all-in-one online Wavelength Calculator performs calculations using a formula that relates the wave velocity and its frequency to the wavelength. You can enter the values of any two known parameters in the input fields of this calculator and find the missing parameter.
Wavelength Formula
Wavelength is the distance between identical points in the adjacent cycles of a waveform. In other words, it is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings.
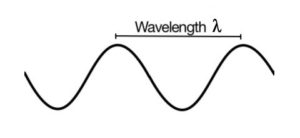
The wavelength depends on the medium (e.g. vacuum, air or water) through which the wave travels. Examples of waves are sound waves in a medium, light propagating in a medium, waves on the surface of water, and periodic electrical signals in a conductor. A sound wave is a change in pressure in a medium (such as air). Light or other electromagnetic radiation is a change in the strength of electric and magnetic fields in space. Waves on water are fluctuations of the water level in a pond.
Wave length is obviously proportional to the speed of wave propagation in space and inversely proportional to the frequency, which is the number of wave cycles per unit time.
In linear media, any wave pattern can be described in terms of independent propagation of sinusoidal components. The wavelength \(λ\) of a sinusoidal signal propagating with constant velocity \(v\) is determined by the expression
$$\lambda = \frac{v}{f},$$
where
\(v\) is the wave’s phase speed (magnitude of the phase velocity),
\(f\) is the wave’s frequency measured in the SI system in hertz (Hz) : 1 Hz = 1 sec -1 .
The phase velocity of a wave in a medium depends on the physical properties of that medium, such as, for example, density of matter and temperature.
In a dispersive medium, the phase velocity itself depends on the frequency of the wave, making the relationship between wavelength and frequency nonlinear. However, in many practical cases, for a wide range of frequencies, the non-linearity can be neglected and the above formula can be used.
The table below shows the velocities for some wave types. You can use these values in your calculations with our Wavelength Calculator.
Related calculators
Check out our other physics calculators such as Kinetic Energy Calculator or Velocity Calculator.